Star Code

#include <iostream>
#include <memory>
using namespace std;

int* multi(int* num1, int size1, int* num2, int size2)
{
	int size = size1 + size2;
	int* ret = new int[size];
	int i = 0;
	memset(ret, 0, sizeof(int)*size);
	//先把两数组分别相乘 
	for(i = 0; i < size2; ++i)
	{
		int k = i;
		for(int j = 0; j < size1; ++j)
		{
			ret[k++] += num2[i]*num1[j];
		}
	}
	//进位 
	for(i = 0; i < size; ++i)
	{
		if(ret[i] >= 10)
		{
			//加上进位 
			ret[i+1] += ret[i] / 10;
			//只留个位 
			ret[i] %= 10;
		}
	}
	return ret;
}
int main(int argc, char *argv[])
{
	int num1[] = {1,2,3,4,5,6,7,8,9,1,1,1,1,1};
	int num2[] = {1,1,1,2,2,2,3,3,3,4,4,4,5,5};
	int* ret = multi(num1, 14, num2, 14);
	for(int i = 27; i >= 0; i--)
	{
		cout << ret[i];
	}
	delete[] ret;
	return 0;
}

计算11111987654321*55444333222111=616096746266157102781891631

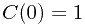
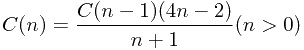
#include <stdio.h>
int C[101][101], len[101];

int main(void)
{
	int i, j, r, t, l;
	C[0][0] = 1;
	len[0]  = 1;
	l       = 1;        //长度
	
	for(i = 1; i <= 100; ++i)
	{
		for(j = 0; j < l; ++j)        //乘法
			C[i][j] = C[i-1][j] * (4*i-2);
		for(r=j = 0; j < l; ++j)
		{
			t       = C[i][j] + r;
			C[i][j] = t % 10;
			r       = t / 10;
		}
		while(r)
			C[i][l++] = r % 10, r /= 10;
		for(j = l-1, r = 0; j >= 0; --j)        //除法
		{
			t       = r*10 + C[i][j];
			C[i][j] = t / (i+1);
			r       = t % (i+1);
		}
		while(!C[i][l-1])
			--l;
		len[i] = l;
	}
			
	for(i = 1; i <= 100; ++i)
	{
		printf("%d:", i);
		for(j = len[i]-1; j >= 0; --j)
			printf("%d", C[i][j]);
		putchar(10);
	}
	
	return 0;
}

/*高精度除法器 v0.1 Author:star date:2010
*可以计算无限循环小数，循环部分用括号表示

*因为整数除法最终肯定会循环，所以输出是有穷的
*一些例子：
*1/3 = 0.(3)
*22/5 = 4.4
*1/7 = 0.(142857)
*2/2 = 1.0
*3/8 = 0.375
*输入格式：数字1+/字符+数字2+回车 
*输入例子：45/56
*输出结果：0.803(571428)
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <assert.h>
#include <memory.h>
#define  BIT 100000 //除数与被除数范围都为100000 

int main(void)
{
	int N, D, Mods[BIT+100];
	char Ans[BIT+100];
	int i, j, st, ed, mod, cnt, Flag, tp , bt;
	char PreChar[100];
NEXT:
	memset(Mods, 0, sizeof(Mods)); //初始化内存 
	memset(Ans,  0, sizeof(Ans));
	memset(PreChar, 0, sizeof(PreChar)); 

	scanf("%d/%d", &N, &D); //输入
  
	assert(N >= 1 && N <= BIT);  //输入限制的数字和范围 
	assert(D >= 1 && D <= BIT);
	Mods[N] = cnt = Flag = 1; //初始化 
	if(!(N % D)) //整除了直接输出
	{
		printf("%d.0\n", N/D);
		goto NEXT;
	}
	if(N < D) //计算小数点前
	{
		PreChar[0] = '0';
		PreChar[1] = '.';
	}
 	else
 	{
 		tp = N / D;
  		bt = log10(tp);
		PreChar[bt+1] = '.';
  		for(i = bt; i >= 0; --i)
  		{
   			PreChar[i] = tp % 10 + '0';
   			tp /= 10;
  		}
  		N %= D;
  		PreChar[i] = '.';
	}
 	i   = 0;
 	mod = 100009; //Magic Number
 	while (!Mods[mod]) {  //计算小数点后的除法
  		Mods[mod] = cnt;
  		++cnt;
  		N        *= 10;
  		Ans[i++]  = N / D + '0';
  		N =  mod  = N % D;
 	} 
 	//寻找开始循环与结束循环
 	ed = cnt - 1;
 	st = Mods[mod];
 	//整除清0
 	if(Ans[ed-1] == '0' && Mods[0])
 	{
  		Flag      = 0;
  		Ans[ed-1] = '\n';
 	}
 	//输出
 	printf("%s", PreChar);
 
 	for(j = 0,i = 1; i < st; ++i)
  		if(Ans[i-1])
  			printf("%c", Ans[i-1]);
 	if(Flag) 
  		printf("(");
 	for(j = i; Ans[j-1]; ++j)
  		printf("%c", Ans[j-1]);
 	if(Flag) 
  		printf(")\n");
 	goto NEXT;
}