Star Code

对于平面上N个点，求其中两个距离最近的点。输入格式：点的个数N，然后是N个坐标即可计算出。

#include <stdio.h>
#include <math.h>
#include <assert.h>
#include <stdlib.h>

struct pos {double x, y;};
typedef struct pos Pos;
Pos p[100000];
int d[100000];
double eps = 0.00001;

int cmp_x(const void *p, const void *q)
{
	double tmp=((Pos*)p)->x-((Pos*)q)->x;
	if(tmp>0) return 1;
	else if(fabs(tmp)<eps) return 0;
	else return -1;
}

double Dest(Pos p2, Pos p1)
{
    return ((p2.y-p1.y)*(p2.y-p1.y)+(p2.x-p1.x)*(p2.x-p1.x));
}

double Min(double a, double b)
{
    return a < b ? a : b;
}

int cmp(const void *a, const void *b)
{
     return(*(int *)a-*(int *)b);
}

double NSP(int left, int right)
{
    double m1, m2, m3 , res;
    int i, j, ix, mid;
    if(right - left == 1)
        return Dest(p[right], p[left]);
    else if(right - left == 2)
    {
        m1 = Dest(p[left], p[left+1]);
        m2 = Dest(p[left], p[left+2]);
        m3 = Dest(p[left+1], p[left+2]);
        return Min(m1, Min(m2, m3));
    }
    mid = (left+right)/2;
    res = Min(NSP(left, mid), NSP(mid+1, right));
    
    ix = 0;
    for(i = mid; i>=left && p[mid].x-p[i].x < res; --i)
        d[ix++] = i;
    for(i = mid+1; i<=right && p[i].x-p[mid+1].x < res; ++i)
        d[ix++] = i;
    qsort(d, ix, sizeof(d[0]), cmp);
    for(i = 0; i < ix; ++i)
        for(j = i+1; j<ix && j<i+4 && p[d[j]].y-p[d[i]].y < res; ++j)
            res = Min(res, Dest(p[d[j]], p[d[i]])); 
    return res;
}

int main(void)
{
    int N, i;
    while(scanf("%d", &N), N)
    {
    	assert(N!=1 && N<100000);
        for(i = 0; i < N; ++i)
            scanf("%lf %lf", &p[i].x, &p[i].y);
            
        qsort(p, N, sizeof(p[0]), cmp_x);
        printf("%.2lf\n", sqrt(NSP(0, N-1)));
    }
    return 0;
}

用的是分治法。

/*author:Star date:2010-08-02*/
#include <stdio.h>
#include <assert.h>

int CntBit(unsigned int n)	//分治思想
{
	n = ((n & 0xaaaaaaaa) >> 1 ) + (n & 0x55555555);
	n = ((n & 0xcccccccc) >> 2 ) + (n & 0x33333333);
	n = ((n & 0xf0f0f0f0) >> 4 ) + (n & 0x0f0f0f0f);
	n = ((n & 0xff00ff00) >> 8 ) + (n & 0x00ff00ff);
	n = ((n & 0xffff0000) >> 16) + (n & 0x0000ffff);
	return n;
}

int main(int argc, char *argv[])
{
	unsigned int N;
	int i, j;
	scanf("%u", &N);
	printf("%u:", N);
	i = CntBit(N);
	assert(i >= 0 && i <= 32);
	for(j = 31; j >= 0; --j)
		printf("%d", N&(1<<j) ? 1 : 0);	
	printf("\nhave %d bit that are \'1\'", i);
	return 0;
}

这里数以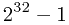的大小范围为例。

/*高精度除法器 v0.1 Author:star date:2010
*可以计算无限循环小数，循环部分用括号表示

*因为整数除法最终肯定会循环，所以输出是有穷的
*一些例子：
*1/3 = 0.(3)
*22/5 = 4.4
*1/7 = 0.(142857)
*2/2 = 1.0
*3/8 = 0.375
*输入格式：数字1+/字符+数字2+回车 
*输入例子：45/56
*输出结果：0.803(571428)
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <assert.h>
#include <memory.h>
#define  BIT 100000 //除数与被除数范围都为100000 

int main(void)
{
	int N, D, Mods[BIT+100];
	char Ans[BIT+100];
	int i, j, st, ed, mod, cnt, Flag, tp , bt;
	char PreChar[100];
NEXT:
	memset(Mods, 0, sizeof(Mods)); //初始化内存 
	memset(Ans,  0, sizeof(Ans));
	memset(PreChar, 0, sizeof(PreChar)); 

	scanf("%d/%d", &N, &D); //输入
  
	assert(N >= 1 && N <= BIT);  //输入限制的数字和范围 
	assert(D >= 1 && D <= BIT);
	Mods[N] = cnt = Flag = 1; //初始化 
	if(!(N % D)) //整除了直接输出
	{
		printf("%d.0\n", N/D);
		goto NEXT;
	}
	if(N < D) //计算小数点前
	{
		PreChar[0] = '0';
		PreChar[1] = '.';
	}
 	else
 	{
 		tp = N / D;
  		bt = log10(tp);
		PreChar[bt+1] = '.';
  		for(i = bt; i >= 0; --i)
  		{
   			PreChar[i] = tp % 10 + '0';
   			tp /= 10;
  		}
  		N %= D;
  		PreChar[i] = '.';
	}
 	i   = 0;
 	mod = 100009; //Magic Number
 	while (!Mods[mod]) {  //计算小数点后的除法
  		Mods[mod] = cnt;
  		++cnt;
  		N        *= 10;
  		Ans[i++]  = N / D + '0';
  		N =  mod  = N % D;
 	} 
 	//寻找开始循环与结束循环
 	ed = cnt - 1;
 	st = Mods[mod];
 	//整除清0
 	if(Ans[ed-1] == '0' && Mods[0])
 	{
  		Flag      = 0;
  		Ans[ed-1] = '\n';
 	}
 	//输出
 	printf("%s", PreChar);
 
 	for(j = 0,i = 1; i < st; ++i)
  		if(Ans[i-1])
  			printf("%c", Ans[i-1]);
 	if(Flag) 
  		printf("(");
 	for(j = i; Ans[j-1]; ++j)
  		printf("%c", Ans[j-1]);
 	if(Flag) 
  		printf(")\n");
 	goto NEXT;
}

根据斯特林公式：~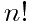

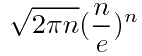
/*calculate the number of digits in the factorial of the integer N.date:2010-07-31*/
#include <stdio.h>
#include <math.h>
#include <assert.h>
int main(void)
{
	const double PI = acos(-1.0);
	int T;
	while(1)
	{
		scanf("%d", &T);
		assert(T > 0 && T < (1<<30));
		printf("%d\n", (int)((T*log(T) - T + 0.5 * log(2*T*PI) ) / log(10)) + 1);
	}
	return 0;
}

#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[])
{
	printf("Hello, World!\n");
	return EXIT_SUCCESS;
}